Equivalence Classes and Circular Counting
This article is useless, wanna know why? Because you already know how to do modular arithmetic even if you’ve never heard of it before. In fact, I bet you use it all the time.
Let me show you.
The Old-Fashioned Way
First I want you to go back…way, way, waaaaaay back to when you very first learned long-hand division. Now I bet your primary school teacher didn’t walk in and say “hey kiddos, today I’m going to show you how long division is also modular arithmetic,” but it’s the truth.
Let’s start with a simple problem.

To solve this problem all you need to do is divide 11 by 4 the old-fashioned way.
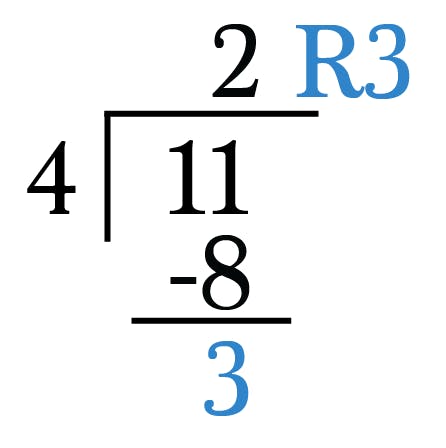
old-school long division
Remember how your teacher used to have you write “R3” at the top for “remainder 3." Later on you learned more sophisticated ways of expressing that extra amount like decimals and fractions, but for modular arithmetic that little ole remainder guy is exactly what we want.
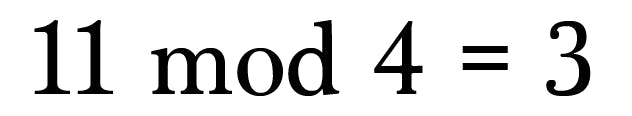
Yep, A mod B is the same as saying “how much is left over when you divide A by B.”
That’s all there is to it! Simple right?
Modulus Time
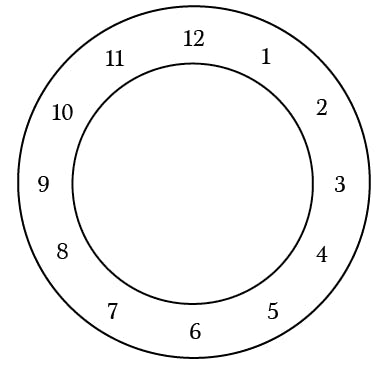
See that clock on the wall?
It’s modulus 12.
Why? Because the standard method for telling time is to split the day into two 12 hour segments. Instead of counting up to 24, we count to 12 twice.
In fact, circular counting is a fundamental representation of modular arithmetic.
Furthermore when you convert between military time and standard time, you’re performing modular arithmetic. For example, we know that 15:00 is the same as 3:00pm because when we divide 15 by 12, we’re left with 3 as a remainder.
So let me posit this: what time would it be right now in a universe that used modulus 8 in their time system?
As I’m writing this it’s 10pm. In a universe that uses modulus 8, the time would be 6 o’clock.
(solution: 10pm is the 22nd hour of the day. So we take 22 mod 8. Eight of course goes into 22 twice with a remainder of 6. That means 22 mod 8 = 6.)
Equivalence Classes
Now your probably thinking that modular arithmetic is kinda useless because you keep getting the same answers over and over again.
You’re right! In fact that’s the beauty of modular arithmetic. It gives us a new way to relate numbers to one another.
Check this out.
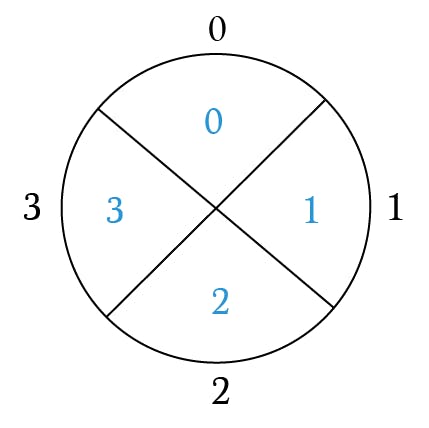
Let’s represent modulus 4 with the following circle diagram.
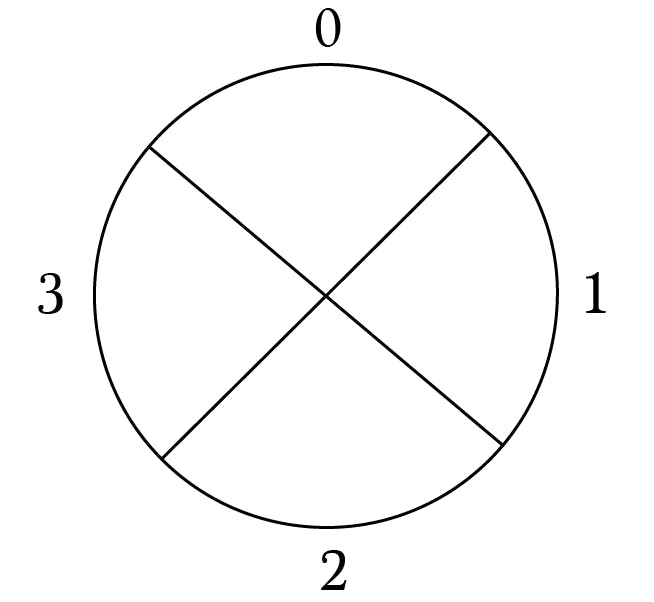
Recall that when you divide by 4, you have 4 possible remainders: 0 (aka no remainder), 1, 2, and 3.
Let’s calculate 0, 1, 2 and 3 mod 4:
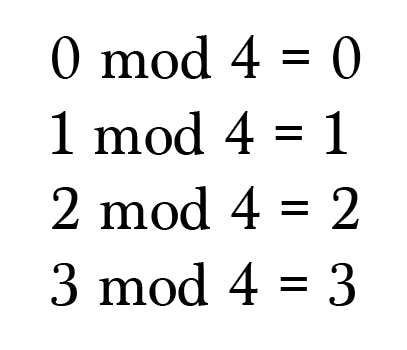
Place the numbers in their respective sections of the modulus 4 diagram.
And continue calculating:
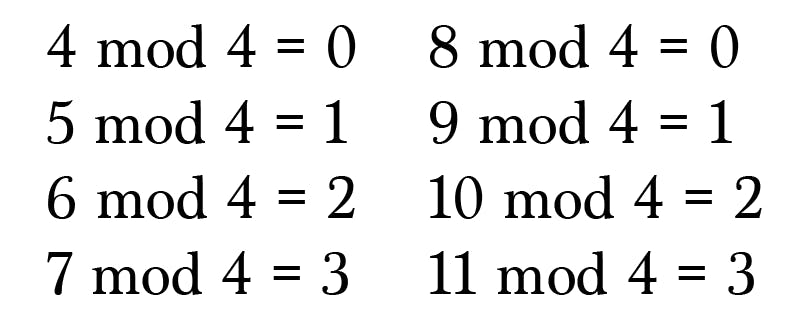
Add these numbers to the diagram:
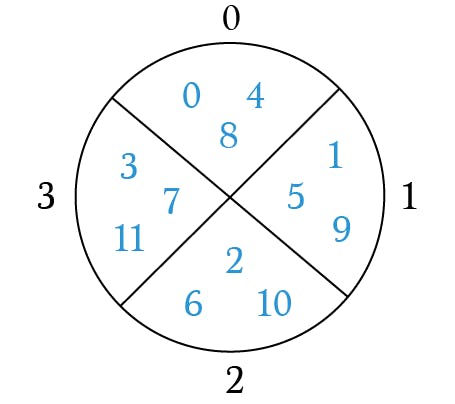
Each of these sections represents an equivalence class.
For example we could say:
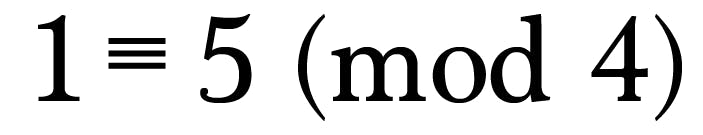
read: 1 is congruent to 5 in modulus 4
Since 1 and 5 are in the same equivalence class (i.e. they both have a remainder of 1 when divided by 4) they’re congruent.
Furthermore, we can write formulas for each equivalence class of modulus 4:
- Values in the “0” equivalence class are multiples of 4 → 4x
- Values in the “1” equivalence class are multiples of 4 plus 1 → 4x + 1
- Values in the “2” equivalence class are multiples of 4 plus 2 → 4x + 2
- Values in the “3” equivalence class are multiples of 4 plus 3 → 4x + 3 where x = 0, 1, -1, 2, -2, and so forth
There you go! The basics of modular arithmetic, and you see it’s actually quite elementary.
Thanks For Reading.
Mostafa Hassanein
